Exitos y estoy atento a sus comentarios.
Factorización
En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
Factorizar un polinomio
Antes que todo, hay que decir que todo polinomio se puede factorizar utilizando números reales, si se consideran los números complejos. Existen métodos de factorización, para algunos casos especiales.
- Binomios
- Diferencia de cuadrados
- Suma o diferencia de cubos
- Suma o diferencia de potencias impares iguales
- Trinomios
- Trinomio cuadrado perfecto
- Trinomio de la forma x²+bx+c
- Trinomio de la forma ax²+bx+c
- Polinomios
- Factor común
Caso I - Factor común
Sacar el factor común es añadir la literal común de un polinomio, binomio o trinomio, con el menor exponente y el divisor común de sus coeficientes, y para sacar esto, hay una regla muy sencilla que dice: Cuadrado del primer término más o menos cuadrado del segundo por el primero más cuadrado del segundo, y no hay que olvidar, que los dos que son positivos iguales funcionan como el primer término, sabiendo esto, será sumamente sencillo resolver los factores comunes.
Factor común monomio
Factor común por agrupación de términos

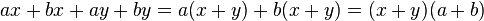
Factor común polinomio
Primero hay que determinar el factor común de los coeficientes junto con el de las variables (la que tenga menor exponente). Se toma en cuenta aquí que el factor común no solo cuenta con un término, sino con dos.un ejemplo:
VIDEO
Aquí tienen un video para clarificar aún más el primer caso de factorización.
EJERCICIOS
Para realizar ejercicios de práctica del primer caso de factorización puedes dirigirte al Algebra de Baldor o seguir los siguientes enlaces:
http://ejercicioscasosdefactorizacion.blogspot.com/2008/10/ejercicios-de-los-5-primeros-casos-de.html
http://es.scribd.com/doc/40098/GUIA-EJERCICIOS-DE-FACTORIZACION
Para realizar ejercicios de práctica del primer caso de factorización puedes dirigirte al Algebra de Baldor o seguir los siguientes enlaces:
http://ejercicioscasosdefactorizacion.blogspot.com/2008/10/ejercicios-de-los-5-primeros-casos-de.html
http://es.scribd.com/doc/40098/GUIA-EJERCICIOS-DE-FACTORIZACION
Espero que este material te haya servido de apoyo para solucionar dudas y afianzar tus conocimientos. Estoy atento a sus comentarios.







http://www.youtube.com/watch?v=xGh8-CCKpaM&list=PLC828A452A9287BB2
ResponderEliminarGRACIAS
ResponderEliminaresta bien
ResponderEliminarGENIAL AMIGO ESPERO LOS DEMAS CASOS PORFA ME AYUDASTE VASTANTE AMIGO
ResponderEliminar